http://www.hispajuegos.net/juegos/logica/1469/Arithmetic
estos juegos son de sumas,restas, multiplicaciones y divisiones .
sábado, 8 de septiembre de 2012
Las ecuaciones aditivas tienen la forma a + x = b, y las ecuaciones multiplicativas tienen la forma a • x = b.
Para resolver ecuaciones aditivas se usa la propiedad de las igualdades, que textualmente dice que “cuando se suma o resta el mismo número en ambos miembros de una ecuación, la igualdad se mantiene”.
Para resolver ecuaciones multiplicativas se aplica la propiedad que dice que “si se multiplica o divide por un mismo número a ambos lados de la igualdad, ésta se mantiene”. Es decir: cuando se tiene una ecuación de esta forma, en la cual un número se halla multiplicando a la incógnita, se debe dividir a ambos lados de la ecuación por dicho número.
ejercicios de ecuaciones aditivas :
x + 3 = 5 x + 9 = 6 x – 4 = -7 9 = x + 12 1 – 8 = 6 + x – 2 + 4
x + 2 = 7 x + 8 = 2 x – 5 = -9 2 = x - 7 3 – 9 = 4 + x – 7 + 6
Para resolver ecuaciones aditivas se usa la propiedad de las igualdades, que textualmente dice que “cuando se suma o resta el mismo número en ambos miembros de una ecuación, la igualdad se mantiene”.
Para resolver ecuaciones multiplicativas se aplica la propiedad que dice que “si se multiplica o divide por un mismo número a ambos lados de la igualdad, ésta se mantiene”. Es decir: cuando se tiene una ecuación de esta forma, en la cual un número se halla multiplicando a la incógnita, se debe dividir a ambos lados de la ecuación por dicho número.
ejercicios de ecuaciones aditivas :
x + 3 = 5 x + 9 = 6 x – 4 = -7 9 = x + 12 1 – 8 = 6 + x – 2 + 4
x + 2 = 7 x + 8 = 2 x – 5 = -9 2 = x - 7 3 – 9 = 4 + x – 7 + 6
ejercicios de ecuaciones multiplicativas :
2x = 8 3x = 21 4x = 20 5x = 80 6x = 120 7x = 1
2x + 9 = 19 3x + 7 = 22 4x + 5 = 37 5x + 13 = 23 6x + 24 = 72
2x – 1 = 5 4x – 2 = 6 3x – 4 = 23 5x – 10 = 30 6x – 45 = 15
2x - 8 + 6 = 8 3x + 4 – 9 = 10 4x – 3 + 7 = 2 9 – 5 5x + 3 – 5 = 70 - 27
Problemas de ecuaciones
PRIMER PROBLEMA
Un empresario ha comprado doble número de Computadoras portátiles que de computadoras fijas. Por cada portátil pago $5,800 y por cada fija $14,500.00 Si el importe de la compra fue de $ 130,500.00¿Cuántas portátil compró y cuantas fijas?
Si
x = número de computadoras fijas
Entonces
2x = número de computadoras portátil
Así que:
2x(5800) + 14500x = 130 500
11600x + 14500= 130500
26 100 x = 130500
26 100 x = 130500
x = 130500/26100
x = 5 Número de fijas
2x = 10 Número de portátiles.
2x = 10 Número de portátiles.
10(5800) + 5(14500) =130 500
58 000 + 72500 = 130 500
130500 = 130500
Respuesta : 10 computadoras portátiles, 5 computadoras fijas.
SEGUNDO PROBLEMA :
Encontrar las edades de María y José, si ambas suman 124 años y María tiene 14 años menos que José.
Primera condición:
Edad de María + edad de José = 124 años
M+J = 124
M+J = 124
Segunda condición:
Edad de José – 14 = Edad de María
J-14 = M
Si J = x
Entonces:
x-14= M
x-14= M
Ahora entonces.
Si
M+J = 124
Entonces:
x-14 + x =124
Resolvemos.
x- 14 + x = 124
2x -14 + 14 = 124 +14
2x = 138
2x/ 2 = 138/2
x = 69
Comprobamos.
Segunda condición; María tiene 14 años menos que José.
Si
x = J y J = x entonces J= 69 años.
Entonces
Edad de José – 14 = Edad de María
J-14 = M
69 – 14 = 55
55 = 55
Edad de María 55 años.
Primera condición
Edad de María + edad de José = 124 años
M+J = 124
Si: J = 69 y M = 55
Entonces:
55 + 69 = 124
124 = 124
Respuesta: edad de José 69 años, edad de María 55 años.
TERCER PROBLEMA :
Un negocio de mascotas compro 15 animales entre perros y gatos, cada perro costo $3000.00 y cada gato $1,500.00. Se hizo una inversión total de $30,000.00, ¿ Cuántos perros y cuántos gatos se han comprado? .
Si
x = número de perros, y 15 – x = número de gatos.
Entonces:
3000 x + 1500(15-x) = 30000
3000 x + 22500-1500x = 30000
1500 x + 22500-22500 = 3000 -22500
1500 x = 7500
1500 x / 1500 = 7500 / 1500
x = 5 número de perros.
15 – x = número de gatos
15-5 = 10
Comprobando
5(3000) + 10 (1500) = 30000
15000 + 15000 = 30000
30000 = 30000
Respuesta: Se compraron 5 perros y 10 gatos.
miércoles, 5 de septiembre de 2012
ecuaciones de primer grado
una ecuación es una igualdad donde por lo menos hay un número desconocido, llamado incógnita o variable, y que se cumple para determinado valor numérico de dicha incógnita.
Se denominan ecuaciones lineales o de primer grado a las igualdades algebraicas con incógnitas cuyo exponente es 1 (elevadas a uno, que no se escribe).
Como procedimiento general para resolver ecuaciones enteras de primer grado se deben seguir los siguientes pasos:
1. Se reducen los términos semejantes, cuando es posible.
2. Se hace la transposición de términos (aplicando inverso aditivo o multiplicativo), los que contengan la incógnita se ubican en el miembro izquierdo, y los que carezcan de ella en el derecho.
3. Se reducen términos semejantes, hasta donde es posible.
4. Se despeja la incógnita, dividiendo ambos miembros de la ecuación por el coeficiente de la incógnita (inverso multiplicativo), y se simplifica.
Resolución de ecuaciones de primer grado con una incógnita
Para resolver ecuaciones de primer grado con una incógnita, aplicamos el criterio del operador inverso (inverso aditivo o inverso multiplicativo), como veremos en el siguiente ejemplo:
Resolver la ecuación 2x – 3 = 53
Debemos tener las letras a un lado y los números al otro lado de la igualdad (=), entonces para llevar el –3 al otro lado de la igualdad, le aplicamos el inverso aditivo (el inverso aditivo de –3 es +3, porque la operación inversa de la resta es la suma).
Entonces hacemos:
2x – 3 + 3 = 53 + 3
En el primer miembro –3 se elimina con +3 y tendremos:
2x = 53 + 3
2x = 56
Ahora tenemos el número 2 que está multiplicando a la variable o incógnita x, entonces lo pasaremos al otro lado de la igualdad dividiendo. Para hacerlo, aplicamos el inverso multiplicativo de 2 (que es ½) a ambos lados de la ecuación:
2x • ½ = 56 • ½
Simplificamos y tendremos ahora:
x = 56 / 2
x = 28
Historia del Álgebra
La historia del álgebra comenzó en el antiguo Egipto y Babilonia, donde fueron capaces de resolver ecuaciones lineales (ax=b) y cuadráticas (ax2 +bx=c), así como ecuaciones indeterminadas como x2 +y2 =z2, con varias incógnitas. Los antiguos babilonios resolvían cualquier ecuación cuadrática empleando esencialmente los mismos métodos que hoy se enseñan.
valoración de exp.algebraicas
Cuando se le asigna un valor numérico o literal a cada variable de una expresión algebraica y se resuelven las operaciones indicadas en la expresión, para obtener un resultado o un valor final, se está valorizando una expresión algebraica.
Calculemos el valor numérico de la expresión algebraica 5 a2 __ b 3, considerando que:
a = __ 2
b = 1
Pasos:
Reemplazar cada variable, en este caso las letras a y b, por el valor numérico asignado, __ 2 y 1 respectivamente, en la expresión algebraica.
5 a2 __ b 3
5 · (__ 2)2 __ (1)3
Resolver las potencias
5 · 4 __ 1
Realizar las multiplicaciones y/o divisiones, siempre de izquierda a derecha
20 __ 1
Realizar las sumas y/o restas, siempre de izquierda a derecha.
20 + __ 1
19
Recuerda que cuando se anota 2a, significa que hay una operación de multiplicación entre ellos, es decir, 2 a = 2 · a.
Otro ejemplo:
a = 1 ; b = 3 ; c = 4
Reemplazamos los valores en la expresión algebraica:
= 
Para sumar y restar estas fracciones se debe encontrar el mínimo común múltiplo (m.c.m.); en este caso el m.c.m. es 12.
A continuación se reemplaza este número en el denominador de cada fracción y se amplifica el numerador por el número correspondiente de acuerdo al número de veces que esté contenido.
m.c.m : 12 
lunes, 27 de agosto de 2012
Historia del Álgebra
La historia del álgebra comenzó en el antiguo Egipto y Babilonia, donde fueron capaces de resolver ecuaciones lineales (ax=b) y cuadráticas (ax2 +bx=c), así como ecuaciones indeterminadas como x2 +y2 =z2, con varias incógnitas. Los antiguos babilonios resolvían cualquier ecuación cuadrática empleando esencialmente los mismos métodos que hoy se enseñan.
El lenguaje que usamos en operaciones aritméticas en las que sólo intervienen números se llama lenguaje numérico.
En ocasiones empleamos letras para representar cualquier número desconocido, realizamos operaciones aritméticas con ellas e, incluso, las incluimos en expresiones matemáticas para poder calcular su valor numérico.
El lenguaje que utiliza letras en combinación con números y signos, y, además, las trata como números en operaciones y propiedades, se llama lenguaje algebraico.
La parte de las Matemáticas que estudia la relación entre números, letras y signos se llama Álgebra.
Características del lenguaje algebraico
1.- El lenguaje algebraico es más preciso que el lenguaje numérico: podemos expresar enunciados de una forma más breve.
El conjunto de los múltiplos de 5 es 5 • = {±5, ±10, ±15, ...}.
En lenguaje algebraico se expresa 5 • n, con n un número entero.
2.- El lenguaje algebraico permite expresar relaciones y propiedades numéricas de carácter general.
La propiedad conmutativa del producto se expresa a • b = b • a, donde a y b son dos números cualesquiera.
3.- Con el lenguaje algebraico expresamos números desconocidos y realizamos operaciones aritméticas con ellos.
El doble de un número es seis se expresa 2 • x = 6.
Expresiones algebraicas
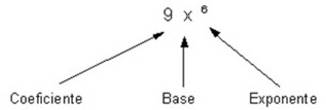
Una expresión algebraica es un conjunto de números y letras que se combinan con los signos de las operaciones aritméticas. Una expresión algebraica se define como aquella que está constituida por coeficientes, exponentes y bases.
Coeficiente numérico: es la cantidad numérica o letra que se encuentra a la izquierda de la base, la cual indica la cantidad de veces que la base se debe sumar o restar dependiendo del signo que tenga.
Ejemplos:
7x4 = x4 + x4 + x4 + x4 + x4 + x4 + x4
– 3x2 = – x2 – x2 – x2
Exponente numérico: es la cantidad que se encuentra arriba a la derecha de la base, la cual indica la cantidad de veces que la base se toma como producto.
Ejemplos:
5x3 = 5 (x) (x) (x)
8( – x + 5)2 = 8(– x + 5) (– x + 5)
Valor numérico de una expresión algebraica
El valor numérico de una expresión algebraica es el número que resulta de sustituir las letras por números y realizar a continuación las operaciones que se indican.
Una cantidad desconocida se puede representar con alguna letra llamada variable.
Suscribirse a:
Comentarios (Atom)